Euclidean Special Relativity

This is a summary of definitions and formulae for computing Euclidean special relativity in the potential energy field. Everything is for collinear motion, because that’s easier and much clearer about what’s going on. No hyperbolic functions are necessary.

Warning! High school level math ahead.

The speed of light (c) = 1

v = velocity as a fraction of c (0 ≤ v ≤ 1).

Lorentz alpha (α) = √(1-v²) = cos(arcsin v) = cos θ = relativistic factor (0 < α ≤ 1).

Lorentz gamma (γ) = 1/α = 1/√(1-v²) = relativistic factor (1 ≤ γ).

Rapidity (p°) = γv = v/α = tan(arcsin v) = tan θ = momentum gradient without the rest mass.

Momenergy (e°) = p°c = γvc = kinetic energy gradient without the rest mass.
When c = 1, momenergy is numerically equal to rapidity.

Gradient angle (θ) = arcsin(v) = arctan(p°) = arctan(e°)

Acceleration = p°_a+b = p°_a + p°_b

The relativistic velocity addition formula:
Your stationary perspective of moving body a's perspective of collinear moving body b:
v_a+b = (v_a+v_b)/(1+v_av_b) = sin(arctan((v_a+v_b)/(cos(arcsin v_a)·cos(arcsin v_b))))
θ_a+b = arctan((tan θ_a / cos θ_b) + (tan θ_b / cos θ_a))
p°_a+b = γ_bp°_a + γ_ap°_b = γ_aγ_b(v_a+v_b)

sin θ = v
cos θ = α
tan θ = p° = sin θ / cos θ = γv

Average kinetic energy (KE°) = ½e° = ½p°c = kinetic energy without the rest mass.
Rest energy = (rest mass)·c² = mc²
Average total energy (E) = rest energy + KE°

Photons, having no rest mass, only have momenergy. They have neither rest energy nor average kinetic energy.

Photons in the Potential Energy Field

Photons, being massless particles that by definition travel at the speed of light, behave differently from massive particles in the potential energy field. They have directional energy, similar to momenergy but without the benefit of resisting lateral motion.

Here we have a photon with 1 unit of energy moving to the right in the potential energy field. Note that all particles have a fixed radius of 1 in the potential energy field.

The energy level about the photon's sphere works similarly to that of a normal particle, (e (1 + cos Φ)) / 2, where e is the photon's energy and Φ is the off-axis angle. This energy distorts the potential energy field as normal, propagating as the simple inverse (1 / x) at the speed of light, which is the speed of the photon itself.

Simplified "top view" diagram of a moving photon's energy gradient over time. There should, mathematically, be an infinitesimal gap rearwards.

Since the photon is already moving at the speed at which change propagates through the field, it creates no gradient in front of itself. Since its energy drops to zero at the trailing edge, it has no gradient directly behind itself, either.

Because the directional energy of a photon is not true momenergy, it reacts to field gradients in a different manner from massive particles. Gradients directly along the axis of motion add to or subtract from the photon's internal energy. Orthogonal gradients alter the photon's trajectory according to the standard vector addition of sin θ, where θ is the gradient angle. However, the photon's tremendous speed means that the shallow gradients of most bodies have relatively little overall effect upon its trajectory.

A gradient angle of 30° = a vector of 0.5c.

A photon's lack of true momenergy means its trajectory is more easily altered than that of a massive particle. Since it has no mass, if its energy is ever reduced to zero, it ceases to exist. Photons never go backwards, but they can change direction. They can even enter elliptical orbits around very massive objects with enormous gradient curvature.

Gravity, Momentum, and the Potential Energy Field

This is a first draft of my paper.  It consolidates the most important points I have come up with in my model of energy, motion, and gravity.

Relativity is based upon just three guiding principles.
A. The speed of light is constant for all observers.
B. Observations made from every inertial reference frame are equally valid.
C. Inertia and gravitational attraction are identical.

To these, I propose adding a fourth:
D. Energy density must be conserved.

This simple addition leads to a model with particles of fixed and finite size in a field of potential energy. The model is more simple and intuitive than general relativity. It also shows a "flattening" of gravitational attraction in low energy areas like the outer regions of rotating galaxies, where general relativity is known to fail.

1. The potential Energy Field

If we are to take seriously the conservation of energy, or more particularly energy density, we must first have something to conserve. That something is the field of potential energy, from which all other fields withdraw their energy. Potential energy is not an abstract bookkeeping term, but a real field with profound impact. But what does this potential energy field look like?

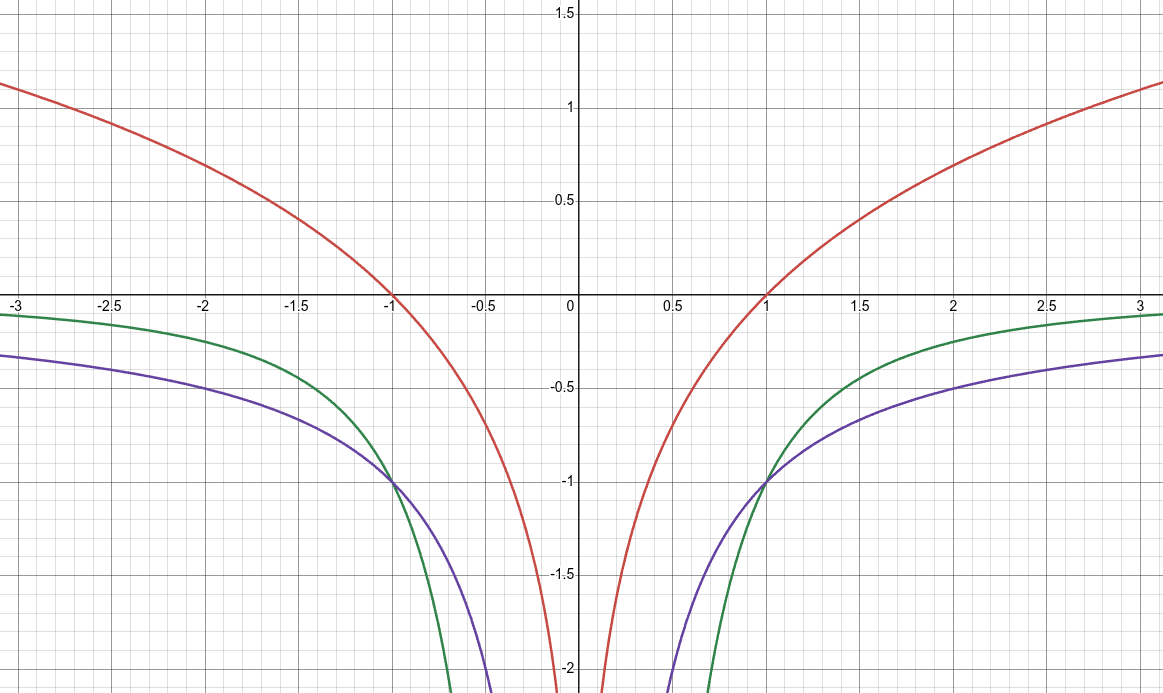
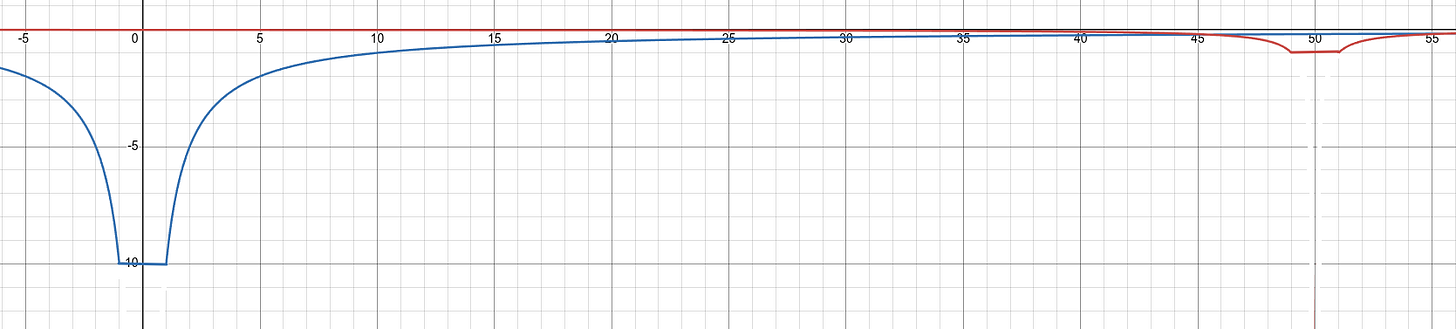
To begin with, the vertical range of the field must go from zero (no potential energy) to some large but fixed and finite number. The graphics throughout this paper show fields with the horizontal representing space and the vertical axis representing potential energy, labeled by how much has been withdrawn.

Red is position -ln|x|, green is velocity -|1/x|, purple is acceleration -|1/x²|.

Looking at the graph above, we clearly see that for a test particle of mass 1, the acceleration and velocity curves cross at x=±1, which is where the position curves cross from positive (external) to negative (internal). Therefore, our particle must have a fixed and finite radius of 1. It withdraws energy proportional to its rest mass.

We shall see that the fixed and finite radius of all particles has profound implications. For one, it eliminates the problem of mathematical infinities and singularities. For another, it allows particles to have an interior wherein local properties may reside.

The potential energy field having a bottom means that black holes are hollow shells of maximal energy density surrounding an absolute nothingness with zero potential energy. It having a top means that calculations with infinite energies are forbidden.

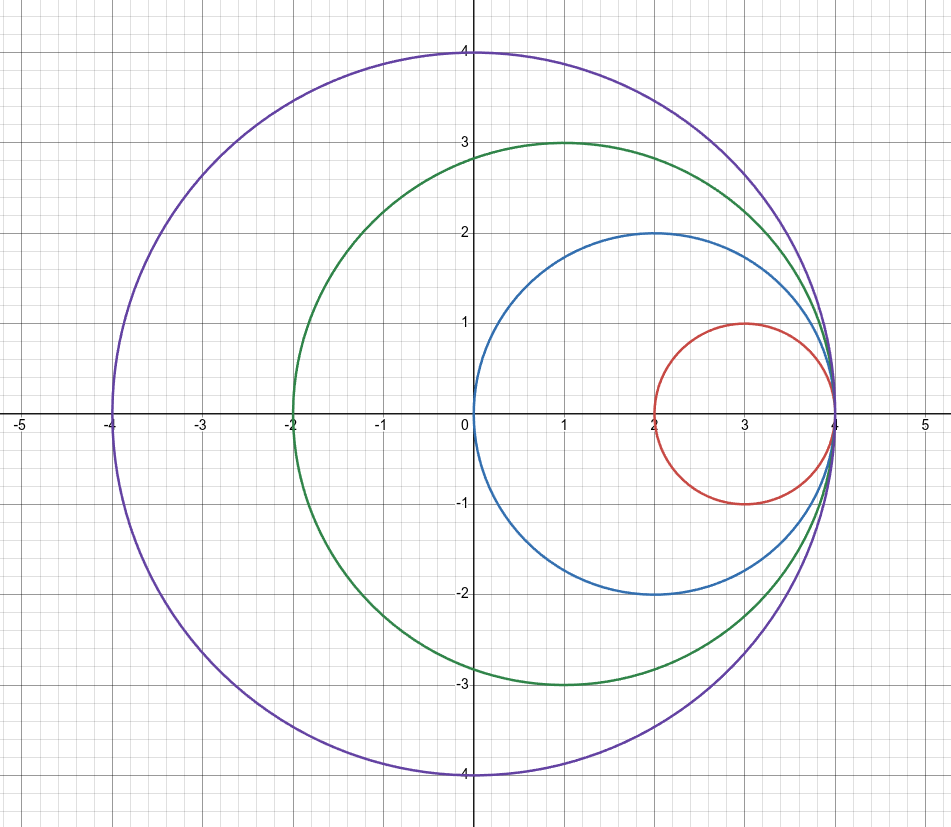
Stationary particles of mass 1 and 10.

Work is that which deforms the potential energy field. It is bound energy.
Rest mass is a form of work that withdraws energy from the potential field evenly across a particle.
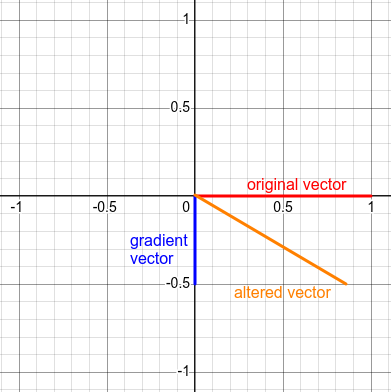
Force is the gradient along the deformations in the field. It is free energy.
The speed of light is the fixed rate at which change propagates through the field.

2. Inertia

Physics makes wide use of the derivative, the slope at a point on a curve, to compute things like force. That simplifies in this model to energy gradients across a particle. Inertia therefore becomes an inherent property of a particle - the energy gradient across its diameter. Thus, the force of gravitational attraction and inertia are exactly the same - energy gradients.

Inertia is the internal energy gradient across a particle.
Gravity is the energy gradient along the field, and is a property external to particles.

These gradients constantly influence each other. "Matter tells space how to bend. Space tells matter how to move." In the absence of a gradient in the field, the particle's gradient, its inertia, will remain unchanged. In the presence of a gradient, the particle's gradient will change in proportion to the gradient and the time spent with that gradient.

3. Gravity

Since particles are not point-like, we cannot use the standard 1/x² force laws. We instead use the calculated gradients. Fortunately, all particles always have the same fixed radius and the field is conservative. That lets us compute a gradient along a curve segment as the difference of the ends of the segment, ignoring everything in between. This is a simplification, as the particle must be physically capable of crossing every subsegment without running out of energy in that direction. A key feature is the radius of the particle r, so the gradient moving to the left from points a to b is calculated from a+r to b-r.

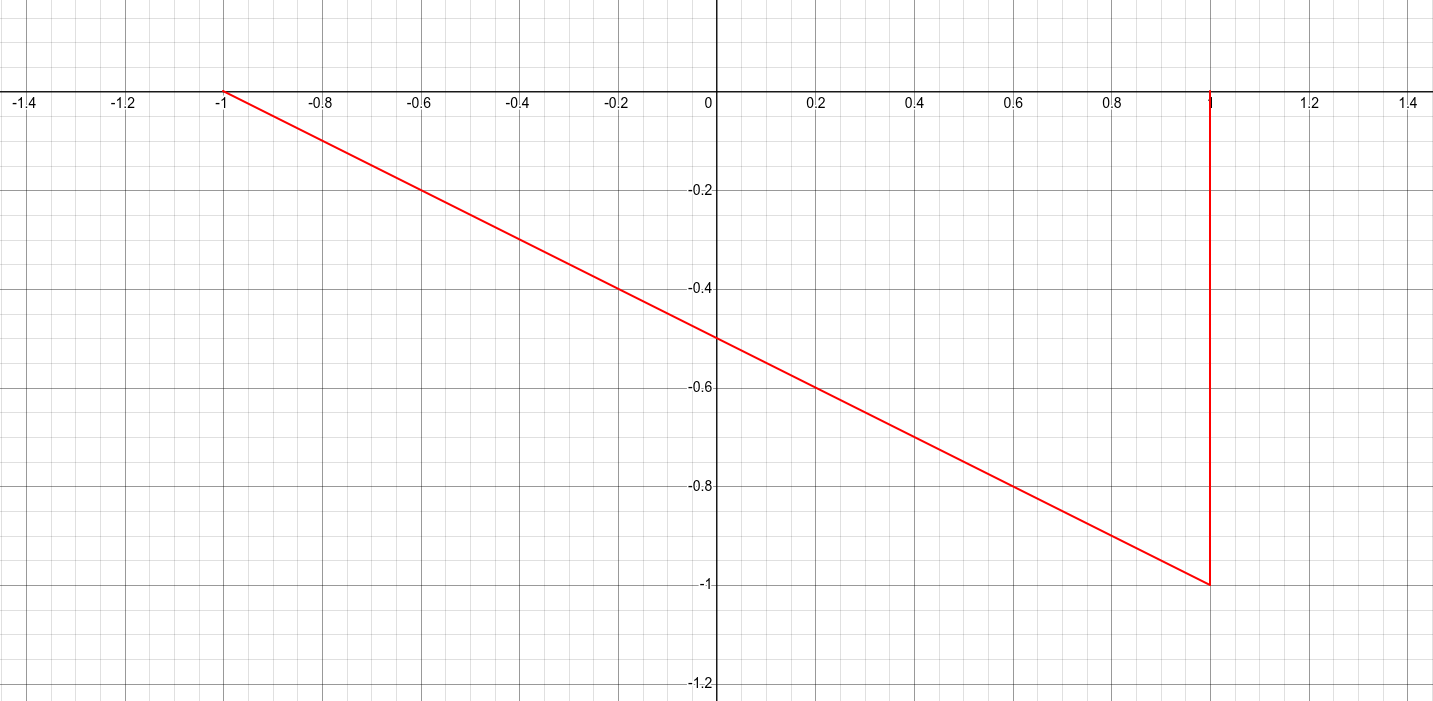
The red particle accelerating towards the blue particle (which is fixed in position to simplify). Particle gradients are intended as visual examples only and are not to any scale.

This overlap replicates the "extra" force of gravity shown in general relativity. The more closely it approaches a massive object, the more the gradient across a particle diverges from the slope at its center. In addition, particles moving slowly along a weak gravitational gradient spend more time being influenced by the same points in the field, effectively "flattening out" the gravitational force in slow/weak areas. This better replicates the rotation of galaxies, a region where general relativity is known to fail.

The red particle is far from the blue, where the gradient is much weaker but always present.

What is the effective gradient felt by particles moving from x=100 to x=40 at different rates?

Number of divisions // Total gradient
1 (Δ=62) // -0.01573
2 (Δ=32) // -0.01615
3 (Δ=22) // -0.01661
4 (Δ=17) // -0.01709
6 (Δ=12) // -0.01806

It's important to recognize that the field altering a particle's energy gradient does not directly effect the field. No energy is lost or gained by the field in this transaction - only the particle changes. Of course, a change in the particle will immediately begin to propagate as a change to the field. But that's an indirect effect, and only to the deformations imposed upon the field by the particle itself.

4. Momentum and Energy, Velocity and Time

Given an energy differential across a particle, how do we determine its properties? What does it mean? We shall use "natural units" throughout, where the speed of light c = 1.

Momentum is the tangent of the gradient angle. This is a conserved, relativistic quantity.
Velocity is the sine of the angle.
The Lorentz alpha factor is the cosine of the angle.
The Lorentz gamma factor is the secant of the angle.

Momentum addition: A_m = B_m + C_m
Gradient addition: A_θ = atan(tan B_θ + tan C_θ)
Velocity addition: A_v = sin(atan(tan(asin B_v) + tan(asin C_v)))

Comparing relative velocities: Stationary observer A sees a ship moving (with respect to A) at speed B. The ship fires a cannonball directly forward along its line of motion moving (with respect to B) at speed C. What speed does A observe the cannonball to have?

A = 0, B = 0.2c, C = 0.3c
A_v = sin(atan(tan(asin 0.2) + tan(asin(0.3)))
= sin(atan(0.204124) + (0.314486)))
= sin(atan(0.518610))
= 0.460380c

To switch reference frames, rotate everything by the appropriate gradient angle, which is the same as subtracting the gradient from everything. In this model, energy differentials are conserved and agreed upon by all observers. The proper time of a particle is essentially irrelevant to the computations, as it is already included in the tangent of the gradient. We don't care about what a particle thinks is going on (so to speak). We're measuring what the energy is doing.

Isn't the gradient an energy gradient? How does it work with momentum? This isn't regular momentum. For one thing, it has nothing to do with the particle's rest mass. This is the momentum of special relativity. When you multiply it by the speed of light (c=1), you get the portion of kinetic energy due to momentum - momenergy. Thus, kinetic energy also has nothing to do with the rest mass of the particle. This handily explains the kinetic energy of a massless photon.

But isn't momenergy a gradient? How, or rather, where do we measure that? You simply take the central point, which is half the total gradient differential. The side directly facing the direction of motion has a total energy of mass + twice the kinetic energy. The side directly opposite has a total energy of just the mass. The central point, orthogonal to the direction of motion, has an energy level of mass + kinetic energy. This is where the total (average) energy is measured.

Average kinetic energy (KE) = half the momenergy = ½ᵧvc.

Average total energy (TE) = rest mass + kinetic energy.

Energy at the edge of a particle at angle Φ from the direction of motion:
TE + KE · cos Φ.

This energy differential, combined with the squeezing and stretching of the field around a particle as it moves relative to the speed of light, results in the familiar blue and red shift effects.