The difference between Newton and Einstein

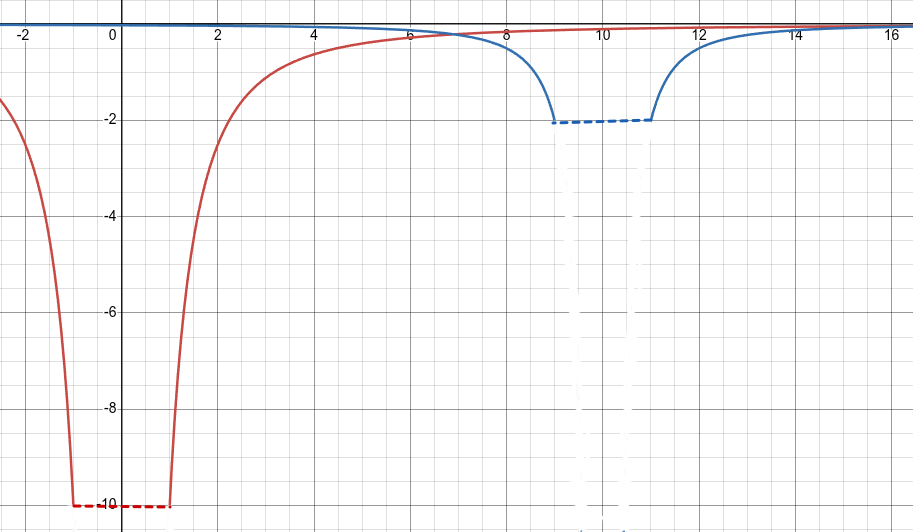
We start, as always, with the energy conserving inverse square function, this time set to represent a stationary particle with a mass of 10.1

Notice that our particle is not exactly point-like. It has a radius of 1.2 The blue dashed line represents its internal gradient, in this case set to zero. Its velocity (sine) is zero (the minimum), while its perception of time and space (cosine, the Lorentz alpha factor) is one (the maximum).

Now, imagine some blue particle being attracted to our red test particle. It has a mass of two, and is moving relatively slowly to the left (its gradient line is slightly lower on the left side). Notice that this blue particle has little effect on the more massive red particle, even at this short range.3 (In future diagrams, I shall hold the red particle stationary through magical means for simplicity.)

Having a lower potential energy on the left side, the blue particle moves in that direction. The gradient created by the red particle across the blue particle adds to this gradient, accelerating the blue particle toward the red. But by how much?

Newton would integrate the force over distance and add it directly to the slope of the particle. This is simple, straight forward, and relatively easy. It is also wrong. If you directly add the slopes, you can get velocities above the speed of light - the speed at which the potential energy field can change. That would tear reality, not to mention bend the gradient curve beyond the 90 degree mark. This way lies madness.

Einstein, remembering that we are working with energy, would add the gradients. Holding the higher (right) end fixed at the mass (-2), decrease the lower (left) end by the amount the red curve changes across the blue particle as it moves. Don’t forget to take into account the time it takes for the blue particle to cross a given amount of space. (Action is the principle of motion here.)

If the blue particle has a gradient of -0.1 (-2.1 left, -2.0 right), and the red particle is exerting a force gradient of -0.1 across the blue particle, then the total gradient across the blue particle becomes -0.2 (-2.2 left, -2.0 right). Notice that would place the energy level at -2.1 at the center of the particle. (Is this why kinetic energy is ½mv²?)

Let us continue the leftward motion of the blue particle. Notice the closer you get to the red particle, the greater the force gradient becomes, so the faster the blue particle accelerates. Let us say that over the next time span, the gradient is -0.4. So the blue particle updates its internal gradient to account for this to -0.6 (-2.6 left, -2.3 center, -2.0 right).

This is a ham-fisted approximation.

Now we must remember that the velocity of a particle is the sine of its internal gradient, while its perception of time and space is the cosine. At this point in spacetime, the blue particle has a gradient of -0.6. Ignoring the sign (which indicates direction), arctan 0.6 is about 30.96 degrees. That makes the velocity (measured in fractions of c) about 0.5145 (154,241,947 m/s) and the alpha contraction about 0.8575. (That’s a gamma factor of about 1.166, for those who prefer it.)

No matter how much it is accelerated, a massive particle can never reach the speed of light, because its gradient will never reach a vertical pitch. Its total energy will be the mass plus the center point of its gradient line (the kinetic energy). Photons emitted in the forward direction will have increased energy (blue shift), while photons emitted backwards will have decreased energy (red shift). Photons emitted 90 degrees to the direction of motion will have have no energy shift, as they originate from the central (total) energy level.4

Addendum:  Newton's solution is approximately correct when the slope is small and thus velocities low, because of the "small x" rule of sines.  When the slope x is small (less than 0.5, 0.5236 radians, 30 degrees), sin(arctan x) ≈ arctan x (or in radians, sin x ≈ x).  The smaller the slope, the closer the congruence.  At a slope of 0.01, the angle is 0.0099996667 radians, the sine of which is 0.0099995000, which is a "mere" 2,997,774.7 meters per second.  The difference between that and 0.01c is only 149.88 meters per second.

Copenhagen interpretation delenda est!

1

Ten what? I don’t know. Somebody smarter than me can probably scale this whole thing so a vertical unit is the reduced Planck constant, h.

2

One what? I don’t know. Somebody smarter than me can probably scale this whole thing so a horizontal unit is a Planck length.

3

Even this fairly small blue gradient across the red particle represents a massive acceleration in normal, everyday life. A 30 degree slope is half the speed of light.

4

An observant reader will note that total energy is not conserved. Energy density is. Our physics professors lied to us, hand-waving away the conversion of potential to kinetic energy. After the conversion, the potential energy is still there, waiting for something else to use it! This is the fundamental difference between (free) energy and (bound) work.